Fourier Transformation of Heviside Function

-

Given that  

show that

Hence, deduce that

Further, deduce that

Solution:

                         
                                                                        
                                   
                                   

The series expansion of

From duplication formula, we have

Therefore, we have

Substituting for  cos(st) in Equation (1) ,we have

                            
 
 
         

                                 
                                         
       

                                
          

From the definition of Bessel function of first kind, we have

Rewriting the result, we have

                                                   

                                  
          

Therefore,

   
                                     

                                     

Applying the inverse Fourier transform, we have

                               

Interchanging s and t, we get

                                

                               
             














 

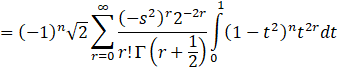
Comments

Post a Comment

Popular posts from this blog

TAM3B - Differential equations

-
Image
  ( x - y ) dx -( x + y ) dy =0 Exact Equation If the first order partial derivatives of M( x,y ) and N( x,y ) are continuous then M dx + N dy = 0 is an exact equation if and only if  ∂ M/ ∂ y = ∂ N/∂ x Hence to solve the exact equation  M dx + N dy = 0   Integrate M with respect to x keeping y constant Integrate those terms in N not containing  x  with respect to   y The sum of those two integrals equated to c is the solution. EXAMPLE 1 ( x^2-2xy+3y^2 )dx+(y^2+6xy-x^2 )dy=0 EXAMPLE 2 ( 2xy-sec^2⁡x )dx+(x^2+2y)dy=0 EXAMPLE 3 Find the value of ‘ n ’ for which ( x+ye^2xy )dx+nxe^2xy  dy=0    and solve it EXAMPLE 4 ( sin⁡ x. tan⁡ y+1)dx-(cos⁡x.sec^2⁡y )dy=0 EXAMPLE 5 ( e^y+1)  cos⁡ x  dx+e^y  sin⁡x  dy=0
Read more